Internal Designs
Intermediate representation (IR)
Taichi's computation IR is designed to be
- Static-single assignment;
- Hierarchical, instead of LLVM-style control-flow graph + basic blocks;
- Differentiable;
- Statically and strongly typed.
For example, a simple Taichi kernel
import taichi as ti
ti.init(print_ir=True)
@ti.kernel
def foo():
for i in range(10):
if i < 4:
print(i)
foo()
may be compiled into
kernel {
$0 = offloaded range_for(0, 10) grid_dim=0 block_dim=32
body {
<i32> $1 = loop $0 index 0
<i32> $2 = const [4]
<i32> $3 = cmp_lt $1 $2
<i32> $4 = const [1]
<i32> $5 = bit_and $3 $4
$6 : if $5 {
print $1, "\n"
}
}
}
note
Use ti.init(print_ir=True) to print IR of all instantiated kernels.
note
See Life of a Taichi kernel for more details about the JIT compilation system of Taichi.
Data structure organization
The internal organization of Taichi's data structure is defined using the Structural Node ("SNode", /snōd/) tree system. The SNode system might be confusing for new developers: it is important to distinguish three concepts: SNode containers, SNode cells, and SNode components.
A SNode container can have multiple SNode cells. The numbers of cells are recommended to be powers of two.
- For example,
S = ti.root.dense(ti.i, 128)creates an SNodeS, and eachScontainer has128Scells.
- For example,
A SNode cell can have multiple SNode components.
- For example,
P = S.dense(ti.i, 4); Q = S.dense(ti.i, 4)inserts two components (onePcontainer and oneQcontainer) into eachScell.
- For example,
Note that each SNode component is a SNode container of a lower-level SNode.
A hierarchical data structure in Taichi, dense or sparse, is essentially a tree with interleaved container and cell levels.
Note that containers of place SNodes do not have cells. Instead, they
directly contain numerical values.
Consider the following example:
# misc/listgen_demo.py
x = ti.field(ti.i32)
y = ti.field(ti.i32)
z = ti.field(ti.i32)
S0 = ti.root
S1 = S0.pointer(ti.i, 4)
S2 = S1.dense(ti.i, 2)
S2.place(x, y) # S3: x; S4: y
S5 = S1.dense(ti.i, 2)
S5.place(z) # S6: z
- The whole data structure is an
S0rootcontainer, containing- 1x
S0rootcell, which has only one component, which is- An
S1pointercontainer, containing- 4x
S1pointercells, each with two components, which are- An
S2densecontainer, containing- 2x
S2densecells, each with two components, which are- An
S3place_xcontainer which directly contains ax: ti.i32value - An
S4place_ycontainer which directly contains ay: ti.i32value
- An
- 2x
- An
S5densecontainer, containing- 2x
S5densecells, each with one component, which is- An
S6placecontainer which directly contains az: ti.i32value
- An
- 2x
- An
- 4x
- An
- 1x
The following figure shows the hierarchy of the data structure. The
numbers are indices of the containers and cells.
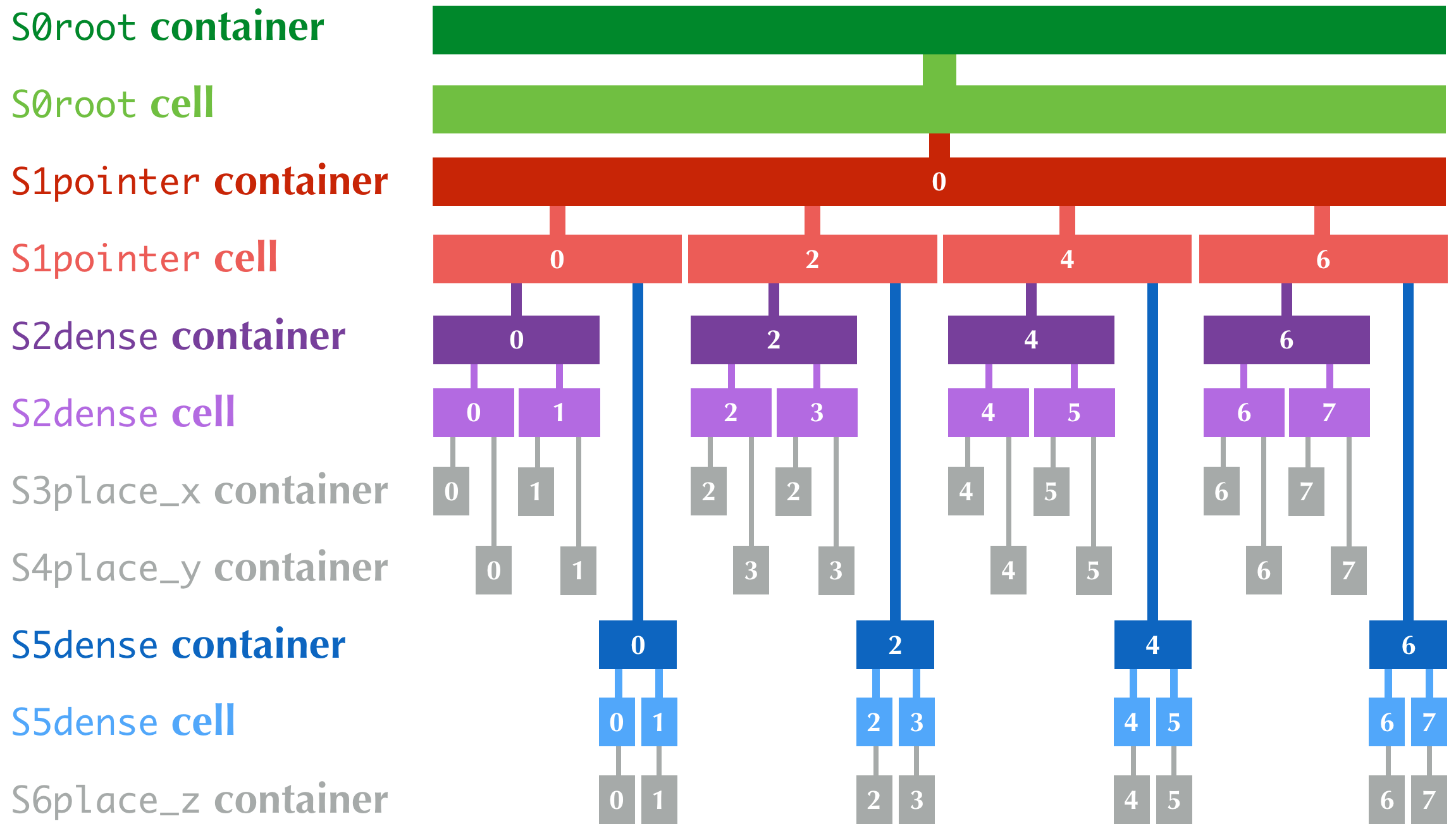
Note that the S0root container and cell do not have an index.
In summary, we will have the following containers:
- 1x
S0rootcontainer - 1x
S1pointercontainer - 4x
S2densecontainers - 4x
S5densecontainers - 8x
S3place_xcontainers, each directly containing ani32value - 8x
S4place_ycontainers, each directly containing ani32value - 8x
S6place_zcontainers, each directly containing ani32value
... and the following cells:
- 1x
S0rootcell - 4x
S1pointercells - 8x
S2densecells - 8x
S5densecells
Again, note that S3place_x, S4place_y and S6place_z containers do not
have corresponding cells.
In struct compilers of supported backends, each SNode has two types: container type and
cell type. Again, components of a higher level SNode cell are
containers of a lower level SNode.
Note that cells are never exposed to end-users.
List generation generates lists of SNode containers (instead of SNode cells).
note
We are on our way to remove usages of children, instances, and elements in Taichi. These are very ambiguous terms and should be replaced with standardized terms: container, cell, and component.
List generation
Struct-fors in Taichi loop over all active elements of a (sparse) data structure in parallel. Evenly distributing work onto processor cores is challenging on sparse data structures: naively splitting an irregular tree into pieces can easily lead to partitions with drastically different numbers of leaf elements.
Our strategy is to generate lists of active SNode containers, layer by
layer. The list generation computation happens on the same device as
normal computation kernels, depending on the arch argument when the
user calls ti.init().
List generations flatten the data structure leaf elements into a 1D list, circumventing the irregularity of incomplete trees. Then we can simply invoke a regular parallel for over the 1D list.
For example,
# misc/listgen_demo.py
import taichi as ti
ti.init(print_ir=True)
x = ti.field(ti.i32)
S0 = ti.root
S1 = S0.dense(ti.i, 4)
S2 = S1.bitmasked(ti.i, 4)
S2.place(x)
@ti.kernel
def func():
for i in x:
print(i)
func()
gives you the following IR:
$0 = offloaded clear_list S1dense
$1 = offloaded listgen S0root->S1dense
$2 = offloaded clear_list S2bitmasked
$3 = offloaded listgen S1dense->S2bitmasked
$4 = offloaded struct_for(S2bitmasked) block_dim=0 {
<i32 x1> $5 = loop index 0
print i, $5
}
Note that func leads to two list generations:
- (Tasks
$0and$1) based on the list of the (only)S0rootcontainer, generate the list of the (only)S1densecontainer; - (Tasks
$2and$3) based on the list ofS1densecontainers, generate the list ofS2bitmaskedcontainers.
The list of S0root SNode always has exactly one container, so we
never clear or re-generate this list. Although the list of S1dense always
has only one container, we still regenerate the list for uniformity.
The list of S2bitmasked has 4 containers.
note
The list of place (leaf) nodes (e.g., S3 in this example) is never
generated. Instead, we simply loop over the list of their parent nodes,
and for each parent node we enumerate the place nodes on-the-fly
(without actually generating a list).
The motivation for this design is to amortize list generation overhead.
Generating one list element per leaf node (place SNode) element is too
expensive, likely much more expensive than the essential computation
happening on the leaf element. Therefore we only generate their parent
element list, so that the list generation cost is amortized over
multiple child elements of a second-to-last-level SNode element.
In the example above, although we have 16 instances of x, we only
generate a list of 4 x S2bitmasked nodes (and 1 x S1dense node).
Statistics
In some cases, it is helpful to gather certain quantitative information
about internal events during Taichi program execution. The Statistics
class is designed for this purpose.
Usage:
#include "taichi/util/statistics.h"
// add 1.0 to counter "codegen_offloaded_tasks"
taichi::stat.add("codegen_offloaded_tasks");
// add the number of statements in "ir" to counter "codegen_statements"
taichi::stat.add("codegen_statements", irpass::analysis::count_statements(this->ir));
Note the keys are std::string and values are double.
To print out all statistics in Python:
ti.core.print_stat()
Why Python frontend
Embedding Taichi in python has the following advantages:
- Easy to learn. Taichi has a very similar syntax to Python.
- Easy to run. No ahead-of-time compilation is needed.
- This design allows people to reuse existing python infrastructure:
- IDEs. A python IDE mostly works for Taichi with syntax highlighting, syntax checking, and autocomplete.
- Package manager (pip). A developed Taichi application and be
easily submitted to
PyPIand others can easily set it up withpip. - Existing packages. Interacting with other python components
(e.g.
matplotlibandnumpy) is just trivial.
- The built-in AST manipulation tools in
pythonallow us to flexibly manipulate and analyze Python ASTs, as long as the kernel body function is parse-able by the Python parser.
However, this design has drawbacks too:
- Taichi kernels must be parse-able by Python parsers. This means Taichi
syntax cannot go beyond Python syntax.
- For example, indexing is always needed when accessing elements
in Taichi fields, even if the fields is 0D. Use
x[None] = 123to set the value inxifxis 0D. This is becausex = 123will setxitself (instead of its containing value) to be the constant123in Python syntax. For code consistency in Python- and Taichi-scope, we have to use the more verbosex[None] = 123syntax.
- For example, indexing is always needed when accessing elements
in Taichi fields, even if the fields is 0D. Use
- Python has relatively low performance. This can cause a performance issue when initializing large Taichi fields with pure python scripts. A Taichi kernel should be used to initialize huge fields.
Virtual indices v.s. physical indices
In Taichi, virtual indices are used to locate elements in fields, and physical indices are used to specify data layouts in memory.
For example,
- In
a[i, j, k],i,j, andkare virtual indices. - In
for i, j in x:,iandjare virtual indices. ti.i, ti.j, ti.k, ti.l, ...are physical indices.- In struct-for statements,
LoopIndexStmt::indexis a physical index.
The mapping between virtual indices and physical indices for each
SNode is stored in SNode::physical_index_position. I.e.,
physical_index_position[i] answers the question: which physical
index does the i-th virtual index correspond to?
Each SNode can have a different virtual-to-physical mapping.
physical_index_position[i] == -1 means the i-th virtual index does
not correspond to any physical index in this SNode.
SNode s in handy dense fields (i.e.,
a = ti.field(ti.i32, shape=(128, 256, 512))) have trivial
virtual-to-physical mapping, e.g. physical_index_position[i] = i.
However, more complex data layouts, such as column-major 2D fields can
lead to SNodes with physical_index_position[0] = 1 and
physical_index_position[1] = 0.
a = ti.field(ti.f32, shape=(128, 32, 8))
b = ti.field(ti.f32)
ti.root.dense(ti.j, 32).dense(ti.i, 16).place(b)
ti.lang.impl.get_runtime().materialize() # This is an internal api for dev, we don't make sure it is stable for user.
mapping_a = a.snode().physical_index_position()
assert mapping_a == {0: 0, 1: 1, 2: 2}
mapping_b = b.snode().physical_index_position()
assert mapping_b == {0: 1, 1: 0}
# Note that b is column-major:
# the virtual first index exposed to the user comes second in memory layout.
Taichi supports up to 12 (constexpr int taichi_max_num_indices = 12)
virtual indices and physical indices.